matplotlib exercises

matplotlib exercises#

import matplotlib.pyplot as plt
import numpy as np

Q1: planetary positions#

The distances of the planets from the Sun (technically, their semi-major axes) are:

a = np.array([0.39, 0.72, 1.00, 1.52, 5.20, 9.54, 19.22, 30.06, 39.48])

These are in units where the Earth-Sun distance is 1 (astronomical units).

The corresponding periods of their orbits (how long they take to go once around the Sun) are, in years

P = np.array([0.24, 0.62, 1.00, 1.88, 11.86, 29.46, 84.01, 164.8, 248.09])

Finally, the names of the planets corresponding to these are:

names = ["Mercury", "Venus", "Earth", "Mars", "Jupiter", "Saturn", 
         "Uranus", "Neptune", "Pluto"]

(technically, pluto isn’t a planet anymore, but we still love it :)

  • Plot as points, the periods vs. distances for each planet on a log-log plot.

  • Write the name of the planet next to the point for that planet on the plot

Q2: drawing a circle#

For an angle \(\theta\) in the range \(\theta \in [0, 2\pi]\), the polar equations of a circle of radius \(R\) are:

\[x = R\cos(\theta)\]
\[y = R\sin(\theta)\]

We want to draw a circle.

  • Create an array to hold the theta values—the more we use, the smoother the circle will be

  • Create x and y arrays from theta for your choice of \(R\)

  • Plot y vs. x

Now, look up the matplotlib fill() function, and draw a circle filled in with a solid color.

Q3: Circles, circles, circles…#

Generalize your circle drawing commands to produce a function,

draw_circle(x0, y0, R, color)

that draws the circle. Here, (x0, y0) is the center of the circle, R is the radius, and color is the color of the circle.

Now randomly draw 10 circles at different locations, with random radii, and random colors on the same plot.

Q4: Climate#

Download the data file of global surface air temperature averages from here: https://raw.githubusercontent.com/sbu-python-summer/python-tutorial/master/day-4/nasa-giss.txt

(this data comes from: https://data.giss.nasa.gov/gistemp/graphs/)

There are 3 columns here: the year, the temperature change, and a smoothed representation of the temperature change.

  • Read in this data using np.loadtxt().

  • Plot as a line the smoothed representation of the temperature changes.

  • Plot as points the temperature change (no smoothing). Color the points blue if they are < 0 and color them red if they are >= 0

You might find the NumPy where() function useful.

Q5: subplots#

matplotlib has a number of ways to create multiple axes in a figure – look at plt.subplots() (http://matplotlib.org/api/pyplot_api.html#matplotlib.pyplot.subplot)

Create an x array using NumPy with a number of points, spanning from \([0, 2\pi]\).

Create 3 axes vertically, and do the following:

  • Define a new numpy array f initialized to a function of your choice.

  • Plot f in the top axes

  • Compute a numerical derivative of f, $\( f' = \frac{f_{i+1} - f_i}{\Delta x}\)$ and plot this in the middle axes

  • Do this again, this time on \(f'\) to compute the second derivative and plot that in the bottom axes

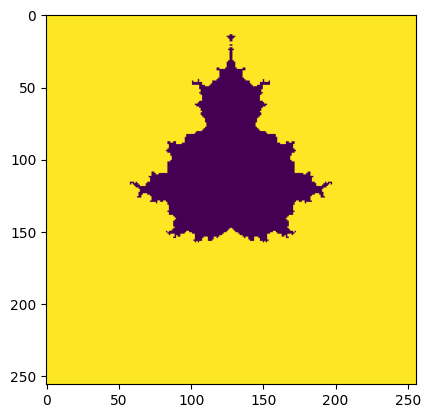
Q6: Mandelbrot set#

The Mandelbrot set is defined such that \(z_{k+1} = z_k^2 + c\) remains bounded, which is usually taken as \(|z_{k+1}| \le 2\) where \(c\) is a complex number and we start with \(z_0 = 0\)

We want to consider a range of \(c\), as complex numbers \(c = x + iy\), where \(-2 < x < 2\) and \(-2 < y < 2\).

For each \(c\), identify its position on a Cartesian grid as \((x,y)\) and assign a value \(N\) that is the number of iterations, \(k\), required for \(|z_{k+1}|\) to become greater than \(2\).

The plot of this function is called the Mandelbrot set.

Here’s a simple implementation that just does a fixed number of iterations and then colors points in Z depending on whether they satisfy \(|z| \le 2\).

Your task is to extend this to record the number of iterations it takes for each point in the Z-plane to violate that constraint, and then plot that data – it will show more structure

N = 256
x = np.linspace(-2, 2, N)
y = np.linspace(-2, 2, N)

xv, yv = np.meshgrid(x, y, indexing="ij")

c = xv + 1j*y

z = np.zeros((N, N), dtype=np.complex128)

for i in range(10):
    z = z**2 + c
    
m = np.ones((N, N))
m[np.abs(z) <= 2] = 0.0

fig, ax = plt.subplots()
ax.imshow(m)

<matplotlib.image.AxesImage at 0x7f30877e7f50>
../_images/2f3d6be234fbbad3bbf3112dabb548ea0967b2c03693392ab305f6f09d5d98b1.png
Contents