SymPy Exercises

import sympy as sym
from sympy import init_session
init_session()

IPython console for SymPy 1.12 (Python 3.11.9-64-bit) (ground types: python)

These commands were executed:
>>> from sympy import *
>>> x, y, z, t = symbols('x y z t')
>>> k, m, n = symbols('k m n', integer=True)
>>> f, g, h = symbols('f g h', cls=Function)
>>> init_printing()

Documentation can be found at https://docs.sympy.org/1.12/

Q1: Creating an expression

Create the expression:

\[f = x e^{-x} + x (1-x)\]

Then evaluate it for

\[x = 0, 0.1, 0.2, 0.4, 0.8\]

Q2: Factoring a polynomial, and finding its roots

Factor

\[x^{4} - 6 x^{3} + x^{2} + 24 x + 16\]

Then find its zeros.

Q3: Integratation and differentiation

Integrate the function:

\[f = \sin(x) e^{-x}\]

Then differentiate the result to see if you get back the original function

Q4: Parsing an expression

Write a program that reads in a mathematical expression as a string (e.g., "sin(2*pi*x)"), converts it to a SymPy expression, and then evaluates it as needed.

Have your program either make a plot of the entered function, or use the input function as the function to fit a dataset to using curvefit.

The following will be helpful:

parse_expr() will convert a string into a SymPy expression

from sympy.parsing.sympy_parser import parse_expr

s = "sin(2*pi*x)"
a = parse_expr(s)
a

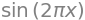
sympy.lambdify() will convert a SymPy expression into a function that is callable by python. You can make it a numpy-compatible function too (this means, e.g., that any sin() in your SymPy expression will be evaluate using np.sin())

f = sym.lambdify(x, a, "numpy")

f(1.0)

#help(lambdify)

Q5: Units

SymPy can deal with physical units. See:

http://docs.sympy.org/latest/modules/physics/units/quantities.html

Let’s try this out. Newton’s 2nd law is

\[F = ma\]

Create a mass of 1 kg and an acceleration of 10 m/s\(^2\), and compute the force, \(F\), and express the result in Newtons.

Note: the convert_to function was added in SymPy 1.1, so if you are using an earlier version, you will need to divide by the target unit to do the conversion.